Unterstützen
Bitte unterstütze mich, wenn dir diese Seite gefällt.
Ergebnis

Wie der Ableitungsrechner funktioniert
Für den technisch interessierten Benutzer folgt eine kurze Erklärung, wie der Ableitungsrechner funktioniert.
Die eingegebene mathematische Funktion wird zunächst durch einen Parser analysiert. Der Parser verwandelt die mathematische Funktion in eine für den Computer besser verarbeitbare Struktur, nämlich einen Baum (siehe Bild unten). Der Ableitungsrechner muss hierbei die Rangfolge verschiedener Operatoren berücksichtigen (z. B. die "Punkt vor Strich"-Regel). Eine Besonderheit bei mathematischen Ausdrücken gilt es ebenfalls zu beachten: Das Multiplikationszeichen wird oft weggelassen, z. B. schreiben wir 5x statt 5*x. Der Ableitungsrechner muss diese Fälle erkennen und das Multiplikationszeichen ergänzen.
Der Parser ist in JavaScript programmiert (basierend auf dem Shunting-yard-Algorithmus) und kann somit direkt im Browser des Benutzers ausgeführt werden. Das ermöglicht eine sofortige Rückmeldung noch während der Eingabe der mathematischen Funktion. Dazu wird aus dem vom Parser generierten Baum eine LaTeX-Darstellung der Funktion generiert. Für die Darstellung im Browser sorgt MathJax.
Wird der "Los!"-Knopf angeklickt, so sendet der Ableitungsrechner die mathematische Funktion in Originalform mitsamt der Einstellungen (Ableitungsvariable und Anzahl der Ableitungen) an den Server. Dort wird die Funktion erneut analysiert. Diesmal wird die Funktion jedoch in eine andere Form umgewandelt, so dass sie vom Computeralgebrasystem Maxima verstanden wird.
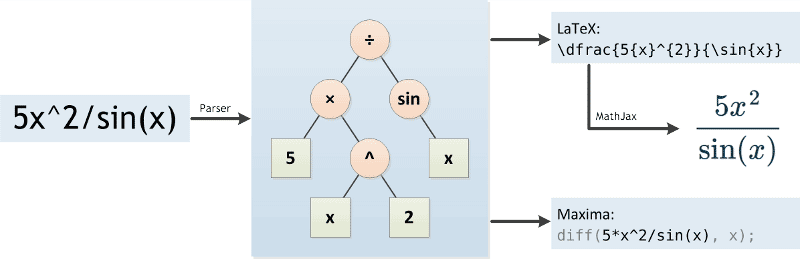
Maxima übernimmt die Berechnung der Ableitungen. Wie jedes Computeralgebrasystem wendet es dazu eine Reihe von Regeln an, um die Funktion zu vereinfachen und nach den allgemein bekannten Ableitungsregeln abzuleiten – so wie man es im Mathematikunterricht lernt. Die Ausgabe von Maxima wird anschließend wieder in LaTeX-Form überführt und dem Benutzer präsentiert.
Das Anzeigen des Rechenwegs ist etwas komplizierter. Hierbei kann der Rechner sich nicht vollständig auf Maxima verlassen, sondern muss die Ableitungen selbst Schritt für Schritt durchführen. Hierzu wurden sämtliche Ableitungsregeln (Produktregel, Quotientenregel, Kettenregel, …) in JavaScript-Code umgesetzt. Für die trigonometrischen Funktionen, die Wurzel-, Logarithmus- und Exponentialfunktion sind die entsprechenden Ableitungen in einer Tabelle gespeichert. In jedem Rechenschritt wird eine Ableitung durchgeführt oder umgeschrieben, z. B. werden konstante Faktoren vor die Ableitung geschrieben und Summen in Ableitungen auseinandergezogen (Summenregel). Letzteres sowie generelle Vereinfachungen der Funktionen werden von Maxima übernommen. Bei jeder durchgeführten Ableitung werden die LaTeX-Codes der dabei entstehenden Ausdrücke im HTML-Code speziell ausgezeichnet, so dass später die farbliche Hervorhebung möglich ist.
Die "Lösung überprüfen"-Funktion hat die schwierige Aufgabe, für zwei mathematische Ausdrücke zu bestimmen, ob diese äquivalent sind. Dazu wird ihre Differenz gebildet und mit Hilfe von Maxima möglichst stark vereinfacht. Hierbei werden z. B. trigonometrische/hyperbolische Funktionen in ihre Exponentialform überführt. Wenn so gezeigt werden kann, dass die Differenz Null ist, dann ist das Problem gelöst. Anderenfalls wird ein probabilistischer Algorithmus angewendet, der die Funktionen an zufällig ausgewählten Stellen auswertet und vergleicht.
Die interaktiven Funktionsgraphen werden im Browser berechnet und in einem Canvas-Element (HTML5) dargestellt. Der Rechner erzeugt hierzu aus der eingegebenen Funktion und den berechneten Ableitungen jeweils eine JavaScript-Funktion, die schließlich in kleinen Schritten ausgewertet wird, um den Graph zu zeichnen. Beim Zeichnen des Funktionsgraphen werden auch Definitionslücken wie z. B. Polstellen aufgespürt und speziell behandelt. Die Gestensteuerung ist mit Hammer.js umgesetzt.
Hast du noch Fragen oder Verbesserungsvorschläge zum Ableitungsrechner? Hat er dir beim Lernen oder bei der Prüfungsvorbereitung geholfen? Gerne kannst du mir eine E-Mail schreiben. Ich freue mich über jedes Feedback!